二分搜索及其边界查找

时隔接近两个月，第二篇vlog

时隔两年的，第一次更新，之前的有点小问题，改了一下，引入了循环不变量的概念。

算法介绍

是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特

定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表

找不到。这种搜索算法每一次比较都使搜索范围缩小一半

算法步骤

1. 首先确定整个查找区间的中间位置 mid = （ left + right ）/2 。

2. 用待查关键字值与中间位置的关键字值进行比较， 若相等，则查找成功　 若大于，则在后（右）半个区域继续进行折半查找　 若小于，则在前

   （左）半个区域继续进行折半查找。

3. 对确定的缩小区域再按折半公式，重复上述步骤。最后，得到结果：要么查找成功， 要么查找失败。折半查找的存储结构采用一维数组存

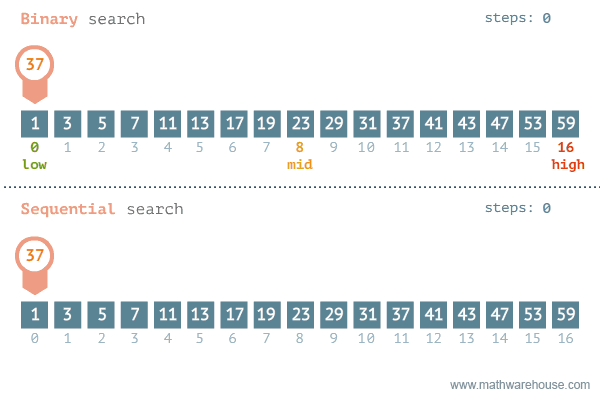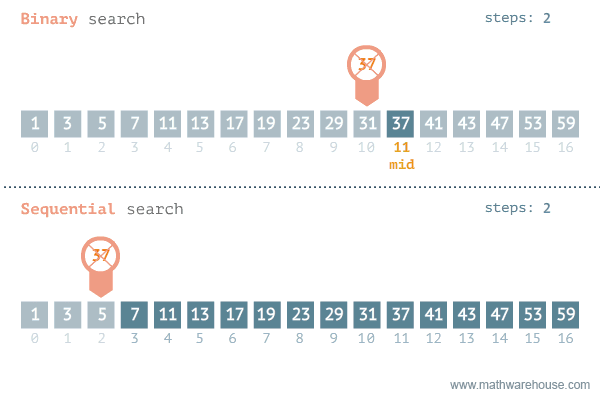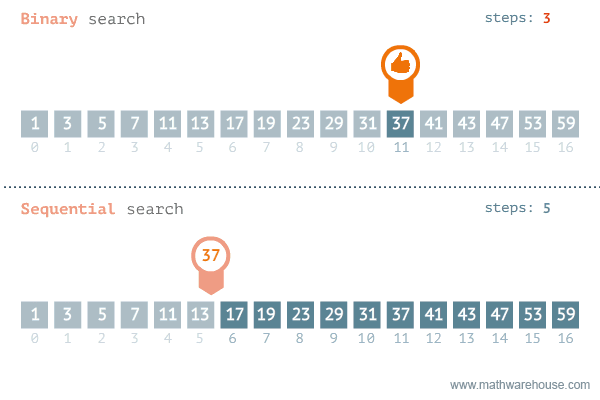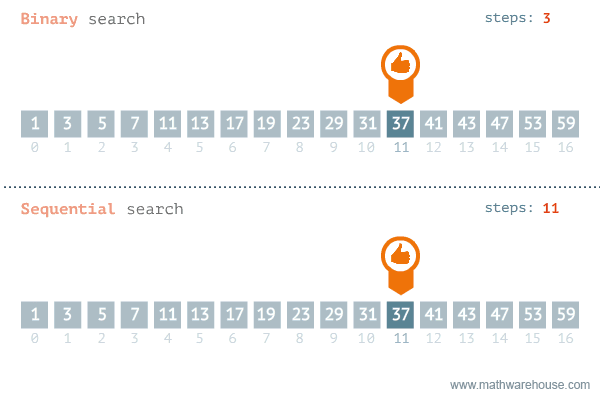
两种模板

二分查找常见的有两种模板

• 左闭右开区间 指的是

  初始条件为 ：left = 0 、right = n

  结束条件为 ：l < r

• 左闭右闭区间 指的是

  初始条件为： left = 0 、right = n-1

  结束条件为 ：l <=r

第一种模板

/**
        左闭右开 [left, right) 结束循环条件为 l < r
 */

public int binarySearch(int[] arr,int target){
    int l = 0, r = arr.length, m;

    while(l < r){
        m = (r - l) / 2;
        if(arr[m] == target){
            return m;
        }else if(arr[m] > target){
            r = m;
        }else{
            l = m + 1;
        }
    }

    return -1;
}

第二种模板

/**
    左闭右开 [left, right] 结束循环条件为 l <= r
 */

public int binarySearch1(int[] arr,int target){
    int l = 0, r = arr.length - 1, m;

    while(l <= r){
        m = (r - l) / 2;
        if(arr[m] == target){
            return m;
        }else if(arr[m] > target){
            r = m - 1;
        }else{
            l = m + 1;
        }
    }

    return -1;
}

如何理解这两种写法

对于第一种写法实际上是 左闭右开区间，实际上指的是在二分数组的时候将数组划分为
[left,mid) 和 [mid, right)

所以说初始条件设置为 left = 0, right = n 结束条件为 l < r 因为 l == r 是 说明此时所有区间已经搜索完了

因此 当 arr[mid] > target 时，说明此时 target 在 [left,mid) 区间中 所以 right = mid

同理 当 arr[mid] < target 时，说明此时 target 在 [mid, right) 区间中，所以 left = mid + 1

对于第二种写法，同理。

二分查找的拓展

第一种模板

/*
	采用左闭右闭区间[left,right)，结束条件为 l < r
	寻找第一个大于等于target的值，
	[1,2,5,5,5,7] target = 5返回第一个5的index
	[1,2,5,7,7,8] target = 6 返回第一个7的index
*/
public int lower_bound(int[] arr,int target){
	int l = 0, r = arr.length, m;
    while(l < r){
       	m = l + (r - l) / 2;
        if(arr[m] < target) l = m + 1;
        else r = m;
    }

    return l;
}


/*
	采用左闭右开区间[left,right)，结束条件为 l < r
	寻找第一个大于target的值，
	[1,2,5,5,5,7] target = 5返回最后一个7的index
*/
public int upper_bound(int[] arr, int target){
	int l = 0, r = arr.length, m;
	while(l < r){
		m = l + (r - l) / 2;
		if(arr[m] <= target) l = m + 1;
		else r = m;
	}
	return  l;
}

第二种模板

/*
	采用左闭右闭区间[left,right],结束条件为 l <= r
	寻找第一个大于等于target的值
	[1,2,5,5,5,7] target = 5返回第一个5的index
	[1,2,5,7,7,8] target = 6 返回第一个7的index
*/
public int lower_bound(int[] arr,int target){
    int l = 0, r = arr.length - 1, m;
    while(l <= r){
		m = l + (r - l) / 2;
        if(arr[m] < target) l = m + 1;
        else r = m - 1;
    }
	return l; // return r + 1
}


/*
	采用左闭右闭区间[left,right]，结束条件为 l <= r
	寻找第一个大于target的值，
	[1,2,5,5,5,7] target = 5返回最后一个7的index
*/
public int upper_bound(int[] arr, int target){
    int l = 0, r = arr.length - 1, m;
    while(l <= r){
        m = l + (r - l) / 2;
        if(arr[m] <= target) l = m + 1;
        else r = m - 1;
    }
	return l; // return r + 1    
}

如何理解

从循环不变式的角度出发，就能够清晰的明白二分的原理。

循环不变式是在循环体的每次执行前后均为真的谓词。循环不变式体现了循环程序中循环变量的变化规律 。

条件：循环不等式，在初始、迭代、终止都恒为真

对于lower_bound,它想查找目标是第一个大于等于target的元素,这里假如target为4，那么结果应该就是箭头所指的元素。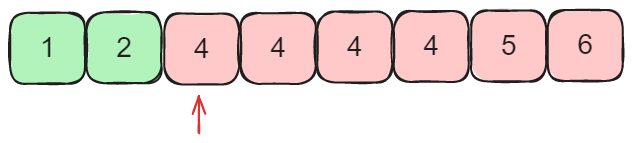

定义循环不变式：l左边的元素是恒小于target，r及r右边的元素是恒大于等于target
定义初始值：l = 0, r = n，满足循环不变式，此时循环不变式覆盖的数组的范围最小。
终止条件：l < r, 即终止时，l == r，此时满足循环不变式，l和r所指向的位置就是我们要找的目标。

当 arr[m] < target 为 true时，我们能够确认的是左区域是小于target，因此 l = m + 1。
当 arr[m] >= target为true时，我们能够确认的是右区域是大于等于target, 因此 r = m
当 l == r时，此时循环结束，l 和 r 指向的就是我们要的结果。

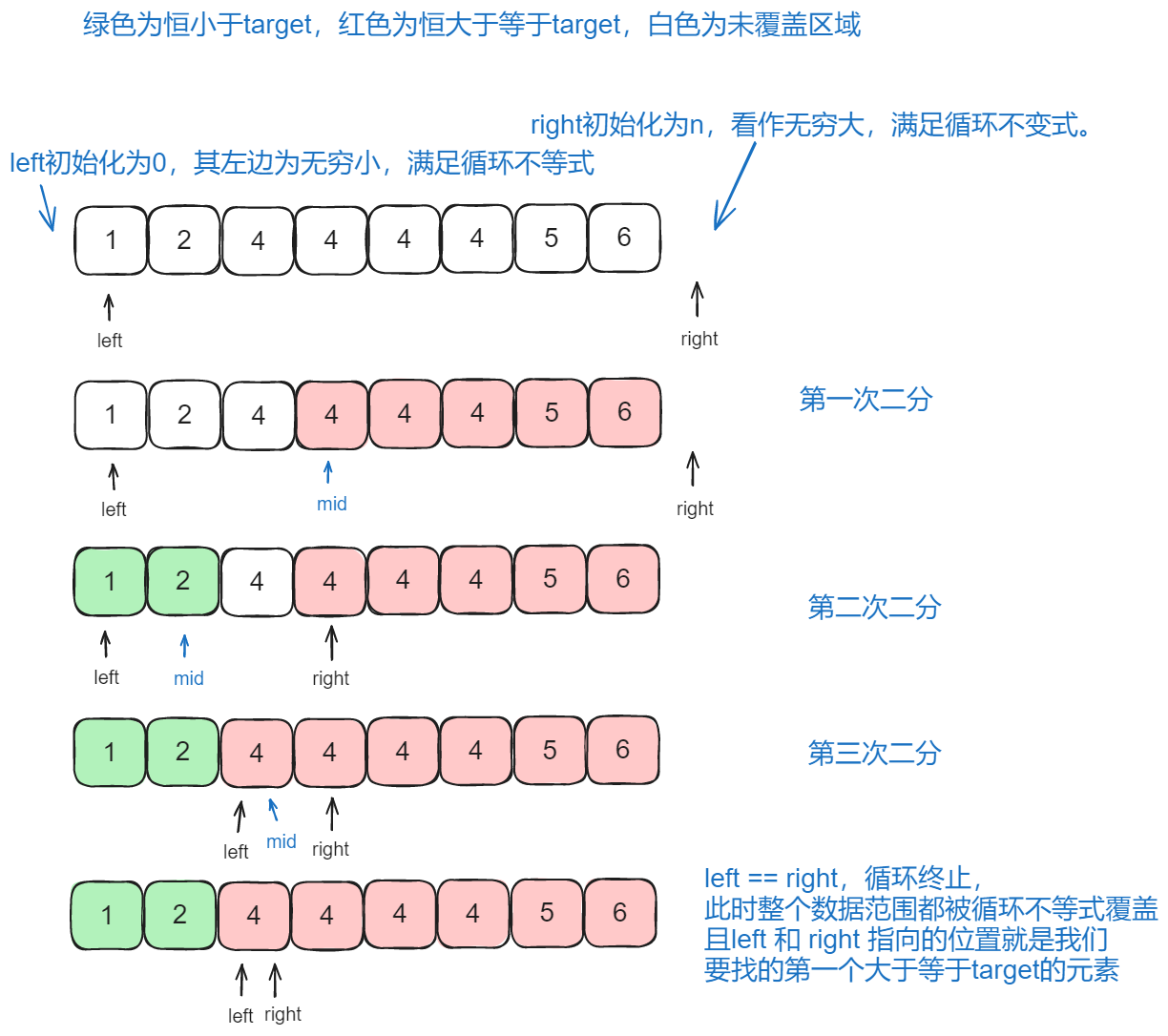
我们可以将这个过程理解为
根据查找目标，设定循环不变式，在二分的过程中，不断扩大满足循环不变式条件的范围，直至将所有数据范围覆盖达到终止。